Maximum Likelihood Estimation (MLE)

MLE를 이해하기 위해서는 먼저, likelyhood function을 알아야 한다.

Likelihood Function 

예를 들어 설명을 하자면, 

 

어떤 확률분포를 통해 데이터 x=[1,4,5,6,7]을 얻었다고 해보자. 

 

그림을 그려보면, 아래와 같이 그릴 수 있습니다. 

 

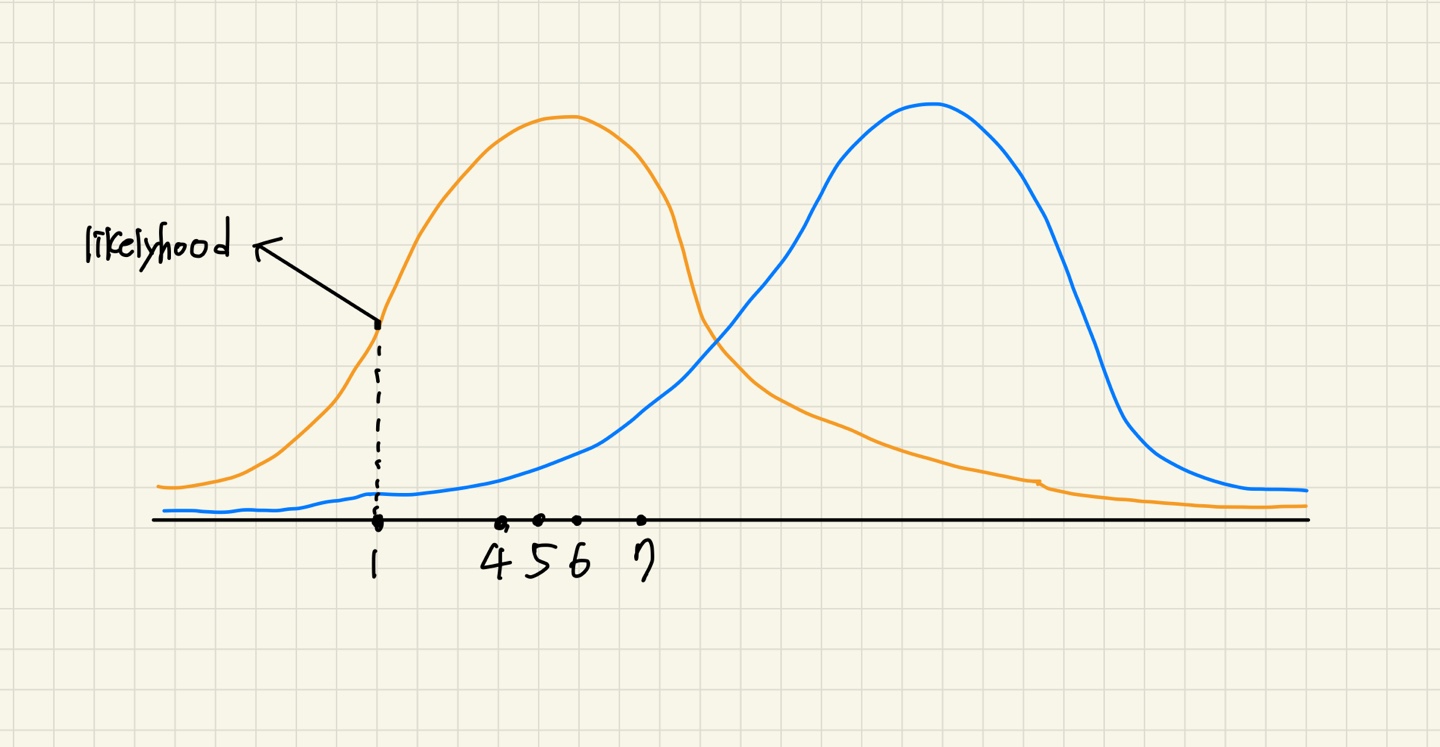
데이터 x가 확률분포에 대응되는 값을 likelyhood라고 합니다.

likelyhood 값을 수식으로 나타내게 되면 아래와 같이 됩니다. 

likelyhood 수식

likelihood function은 위의 likelihood 값들을 모두 곱한 값입니다. 

likelyhood function

 likelyhood function은 모데이터로 부터 데이터를 얻었을 때 어떤 분포로 추출되었을 확률이라고 할 수 있습니다. 

---

 

Maximum Likelihood Estimation 

Maximum Likelihood Estimation은 위의 likelihood function을 최대화 시키는 모분포를 구하는 방법입니다. 

 

즉 아래의 식의 최대 값을 구하는 것이 Maximum likelyhood Estimation이라고 할 수 있습니다. 

likelyhood function

 계산의 편의성을 위해서 log를 취하게 됩니다. 양변에 로그를 취하면

 

로그 likelyhood function

위의 식을 미분 혹은 편미분을 사용하여 최대 값을 구해주면 된다.