GNN(Graph Neural Networks)

Graph

그래프는 일종의 데이터 구조로 objects와 그들의 relationships를 nodes와 edges로 표현한다. 

objects 사이의 관계를 나타내는 데이터를 분석할 때 주로 사용된다.

 

그래프는 주로 Adjacancy Matrix(인접행렬)과 Feature matrix로 표현된다. 

 

Adjacancy Matrix

 

 

 

Feature matrix

 

 

 

 

 

 

그래프는 주로 G = (V,E)로 표현이 되는데 V = node 이고, E는 Edge이다. 위의 그래프는 

G = ({0,1,2,3},{{0,1},{0,2},{1,3}})으로 표현이 가능하다. 

 

GNN이 해결할 수 있는 문제는 크게 3가지로 나눌 수 있다. 

 

• Node Classification 
• Link Prediction
• Graph Classification   

 

Node Classification

Node Embedding을 통해 Node들을 분류하는 문제이다.

아래의 그림과 같이 몇몇의 노드들 만 라벨링 된 상황(파란색 원 , 노란색 원)에서 나머지 노드(검정색 원)를 예측하는 semi supervised learning 방법이다.   

Node Classification

 

Link Prediction 

그래프의 점들 사이의 관계를 파악하고 두 점 사이에 얼마나 연관성이 있을지 예측하는 문제다.

노드 사이에 점선으로 연결된 edge의 연관성을 예측하는 문제이다.

대표적인 예로 Youtube, Netflix의 영상 추천이 있다. 

 

Link Prediction

Graph Classification 

 

그래프 전체를 여러가지 카테고리로 분류하는 문제이다. 이미지 분류와 비슷하지만 대상이 그래프라고 생각하면 된다.

즉 그래프를 인풋으로 받아 해당 그래프의 클래스를 출력하는 문제라고 할 수 있다. 

 

Graph Classification

 

Original Graph Neural Network (Recurrent Graph Neural Network) 

Graph and the neighborhood of a node. The state of the node_1(x_1) depends on the information contained in its neightborhood            Image Source: M.Gori et al. 2005, F.Scaselli et al. 2009 논문 

 

 

 

f: local transition function 

g: local output function 

 

l_n: n의 feature 

l_co[n]: l의 edge 

x_ne[n]: 이웃한 states 들 

l_ne[n]: neighbor nodes의 feature  

 

 

local transition function의 input 값은 해당 노드의 feature, 해당 노드와 연결되어 있는 edge들, 해당 노드와 인접해 있는 다른 이웃 노드들의 states들, 그리고 이웃 노드들의 feature들을 갖는다.  

 

위의 local transition function을 iterative하게(k번) 반복 한다. 

위 과정에서 아래의 이론이 사용된다.

 

Banach's fixed point theorem

   - guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points.

 

즉 k가 크면, x에 매핑 T를 k번 적용한 값과 k+1번 적용한 값이 거의 같다는 의미로 이해하면 된다.

 

k번 반복을 통해서 상태가 충분히 업데이트가 되면 업데이트가 된 마지막 상태와 해당 노드의 feature를 사용하여 결과값(o_n)을 출력한다. 즉, o_n = g_w(x_n, l_n)이 된다.

 

위의 과정을 그림으로 나타내면 

 

위의 그래프를 GNN에 적용시킨다면

 

GNN 적용 

위의 그래프를 더 풀어서 설명해놓은 그림은

 

GNN 연산과정 설명

GNN 알고리즘

 

 

 

 

Loss function

p: number of supervised nodes 

t: target information 

o: output information

Loss function

loss function은 어렵지 않다 

 

---

Graph Convolution Network

 

컨볼루션 신경망의 특징

 

• Learn local features 
• Weight Sharing 

Feature matrix

 

 

위와 같은 그래프에 경우 GCN은 아래의 식과 같이 Hidden State를 업데이트 한다. 

 

Update Hidden State in GCN

 

 

H_0^(l) 의 경우에는 [1 1 1 0]을 값으로 갖는다. 그리고 l(엘)번째 레이어를 통과했을때의 값을 의미한다. 이와 같은 방식으로 연결되어 있는 노드들의 feature 값들을 이용해서 Hidden State들을 업데이트 하게 된다. 하지만 이와 같은 방식으로 계산을 하기에는 계산량이 너무 많다. 그래서 Adjacency Matrix를 이용해준다. 

Adjacency Matrix를 사용해준 식은 아래와 같이 나오게 된다. 

 

 

Update Hidden State with Adjacency Matrix

 

위와 같이 나올 수 있는 이유는 아래의 그림으로 설명이 가능하다. 

 

 

 

Adjacency Matrix에 본인 노드도 연결되어 있는 이유는 자기 자신의 정보도 담아야 하기 때문에 1로 설정을 해주었다. 

위와 같이 Adjacency Matrix를 곱해주면 edge의 연결된 정보 역시 담을 수 있게 된다. 즉 각각의 노드의 이웃한 노드들의 정보을 담고 있는 값들을 받아들여서 컨볼루션 연산을 한 효과를 내게 된다. 

 

Readout - Permutation Invariance 

 

아래와 같은 그림을 보면 같은 그래프이지만, 노드의 순서에 따라서 다른 값이 나올 수가 있다. 이를 방지하기 위해서 

Reaout층을 만들었는데 가장 대표적인 방법이 Node-wise summation 방법이다. Hidden State Matrix를 MLP에 넣어서 Vector로 만들어 준 후에 모두 더해준 후 Activation function τ에 넣어준다. matrix를 Vector로 만들어서 연산을 하기 때문에 아래 두개의 그래프는 같은 값을 갖게 된다.  

Readout 층

전체적인 GCN의 구조를 살펴보면 다음과 같다. 

 

 

 

---

 

Graph Attention Network (GAT) 

 

Graph Attention Network는 중요한 노드에 가중치를 부여하는 Attention을 사용하여 그래프 데이터를 학습하는 딥러닝 모델이다. 

 

i노드와 j노드의 coefficiecny

노드에 self-attention을 적용시켜, i노드와 j 노드의 coefficient를 구할 수 있다. Attention Mechanism a의 인풋으로는 i노드와 j노드에 공유 가중치 W를 곱해준 값들이다. 하지만 위의 식에서는 엣지 정보가 담겨 있지 않다. 그래프에서 의미있게 봐야할 정보는 연결돼있는 노드들이기 때문에 Adjacency Matrix를 사용하여 연결되어 있는 노드들의 coefficiency를 구할 수 있다.이를 Masked Attention이라고 한다. 다른 노드들과의 coefficiency는 쉽게 비교할 수 있기 위해서 softmax함수를 사용해주었다. 

 

Masked Attention

GAT에서 Attention Mechanism a는 1-Layer Feed Forward Neural Network를 사용했다. Activation 함수로는 non-linear한 Leaky ReLU를 사용했다. input으로는 i노드에 가중치 W를 곱한값과 j노드에 가중치 W를 곱한값 들에 concat을 시킨 값이 사용된다. 

 

Leaky ReLU 의 식은 f(x) = max(slope*x,x)이다. Leaky ReLU 같은 경우에는 Dying ReLU 현상을 막기 위해 0대신 slope*x로 바꾼 ReLU이다. GAT 논문에서는 slope=0.2로 설정해주었다. 

 

수식과 그림은 아래와 같다. 

GAT의 Attention Mechanism

위의 과정을 거치고 나면 아래의 수식이 나오게 된다. 

 

 

위의 learning process를 좀 더 stable하게 하기 위해서 Multi-head attention을 사용했다. 아래의 그림은 K=3인 Multi-head Attention을 표현한 그림이다. 서로 독립된 3개의 attention을 concat해주게 된다.  

 

The aggregation process of a multi-head graph attentional layer

아래는 위의 Multi-head attention의 수식이다. 

 

Multi-head Attention

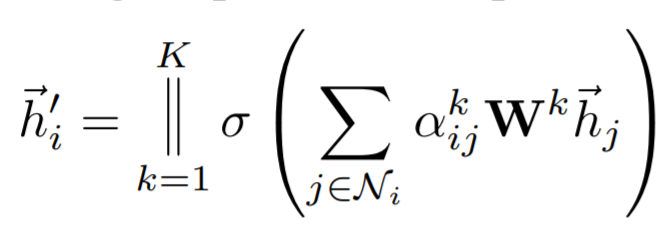
마지막 layer에서는 concat이 무의미해지기 때문에 아래의 식처럼 평균을 구해준다. 

averaging

 

 

Reference 

 

The Graph Neural Network Model Franco Scarselli, Marco Gori, Fellow, IEEE, Ah Chung Tsoi, Markus Hagenbuchner, Member, IEEE, and Gabriele Monfardini, 2009

 

Semi-Supervised Classification with Graph Convolutional Networks, Thomas N. Kipf, Max Welling, 2017

 

Graph Attention NetworksPetar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, Yoshua Bengio,2017